WarpField: portal-casting field-of-view algorithm

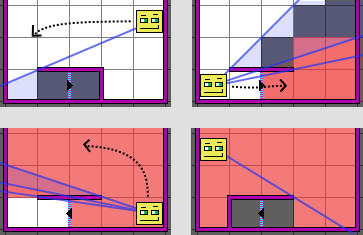
Here's WarpField, a "portal-casting" field-of-view algorithm.  This goes beyond the usual field-of-view mechanism by adding support for portals.  A portal basically connects an edge between tiles in one map with an edge in a (possibly different) map.  WarpField computes the field of view through the portal, and also returns what the player can see at each location.  This could be useful for:

Going up (or down) stairs.

• Continuous overworld movement from zone to zone
• Over/under pathways, such as bridges and tunnels
• Smooth transitions of elevation changes, like stairs
• Crazy magical effects, like portals to alternate dimensions.

In a previous post, I discussed WallyFOV, my implementation of a 2d grid-based field-of-view algorithm using shadow-casting.  For games that don't need portals, that algorithm is a better choice, since it's simpler and faster.  Unlike many field-of-view implementations, WallyFOV supports walls, which is a prerequisite for adding portal support.

"Portal-casting" is basically an extension of shadow-casting.  Shadow-casting tracks contiguous ranges of angles of rays that are visible from the player.  When a wall is encountered, we simply cut that range of angles out (causing a shadow).  For portals, instead of cutting that range out, we split it off into a new, separate range.  For each range we track which map the range "sees", and the relative tile offset into that map.

Entering a tunnel.

For each location that isn't completely in a shadow, we now have to decide which map we're seeing at that location, and which tile in that map goes there.  This can be tricky, because we might see the location more than one way at a time.  Maybe some rays reach the location after passing through a warp to map A, while others reach it after a warp to map B, and some reach it without passing through any warps at all.  In a 2D tile-based game we don't really want to show slices of a tile, we want to just pick one to show.  To resolve this ambiguity, WarpField has an order of preference: rays closest to the center are preferred, followed by rays that go through fewer warps, and finally ties are broken by the map with the lowest "id".

There are a lot of edge cases to consider, and most of them are touched upon in the algorithm overview.  I did a lot of testing and benchmarking, and I'm pretty sure it works according to spec, but there are some asymmetries that I'd like to remove (due to the order in which locations are visited).  I think I can clean that up by switching to fractional math instead of floating-point math.  Nevertheless, it's fairly robust, you can throw crazy cases at it like warps into the same map (such that the player can see themself through it), and rays that pass through many warps at once.

I think this could add a lot of potential to roguelike games.

WarpField (demo)

(github repo)

WallyFOV: Shadow-casting field-of-view implementation with walls

I've been working on a field-of-view algorithm for 2d tile-based games (e.g. roguelikes).  There's a particular killer feature I mean to include in the algorithm, which I won't reveal in this post, but I decided to go ahead and release the slightly simpler version because I think it might be useful on its own.

It's called WallyFOV.  It's basically an implementation of recursive shadowcasting in TypeScript, but with support for walls.

Go ahead and check out the demo.  (and thanks to EasyStar.js for the pathfinding algorithm used in that demo, and from which I kindof copied the demo page style)

Recursive shadowcasting works by scanning outwards from the player looking for obstructions.  When something is found, a shadow (represented by two angles) is added to a shadow list.  Overlapping shadows are merged to keep the algorithm running quickly.

In this particular variant, a tile is considered visible if there exists any line from the center of the player's tile to any point within the target tile.  There are some complications around dealing with diagonally-adjacent bodies, which you can read about in the algorithm overview, but overall it's a pretty simple algorithm to understand.  It's a bit tricky to implement and optimize, however.

I spent a little extra time optimizing it to run in V8 (at least the version of V8 in node.js 7.9).  Along the way I learned how to use node's --trace-deopt, and discovered some very unexpected optimization tips, mainly having to do with newer ECMAScript features.

For instance, this version of V8 doesn't optimize "compound let/const assignment".  Meaning if you declare a variable with let or const, and then use something like X += Y, your function will be deoptimized.  Simply using X = X + Y instead avoids that trap.  The general lesson here is that JavaScript is apparently changing too rapidly to rely on the engine optimizing things according to your intuition.  This is probably true with any language, to a certain extent.  But, come on, X = X + Y?

WallyFOV (demo)

(github repo)